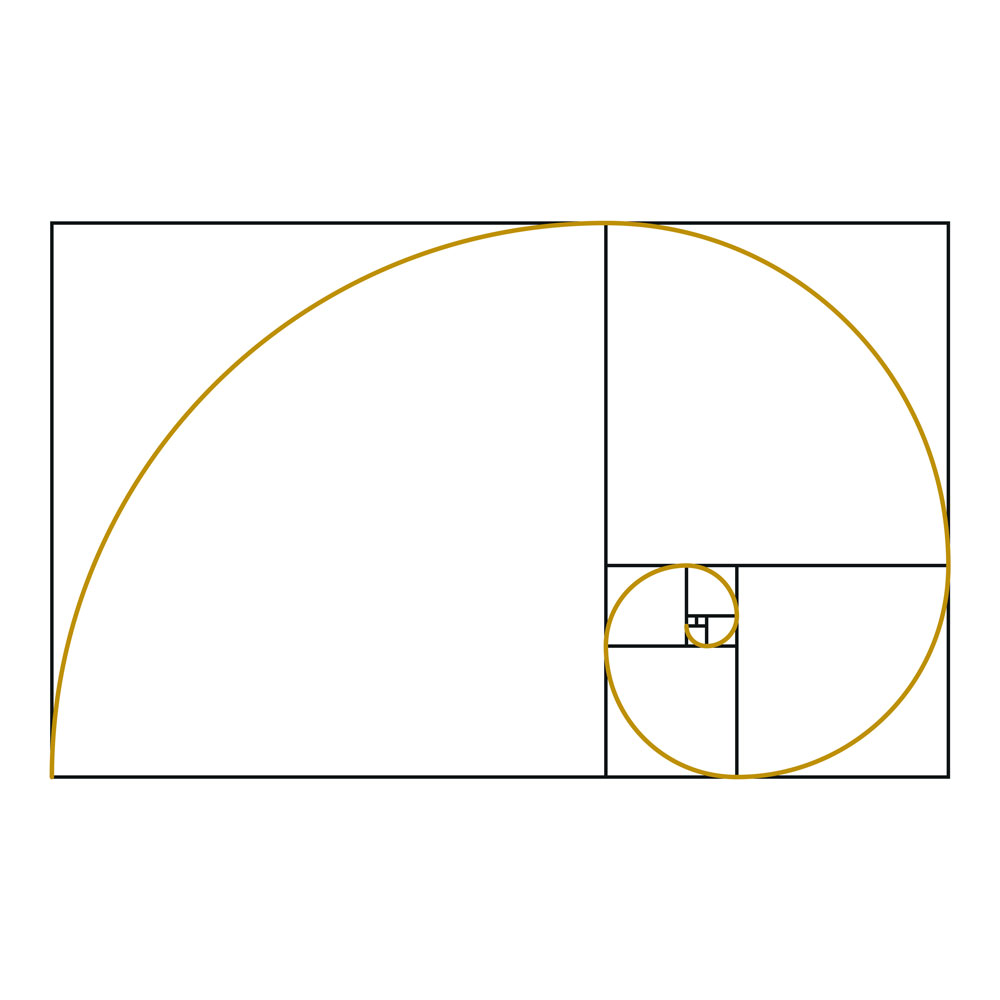
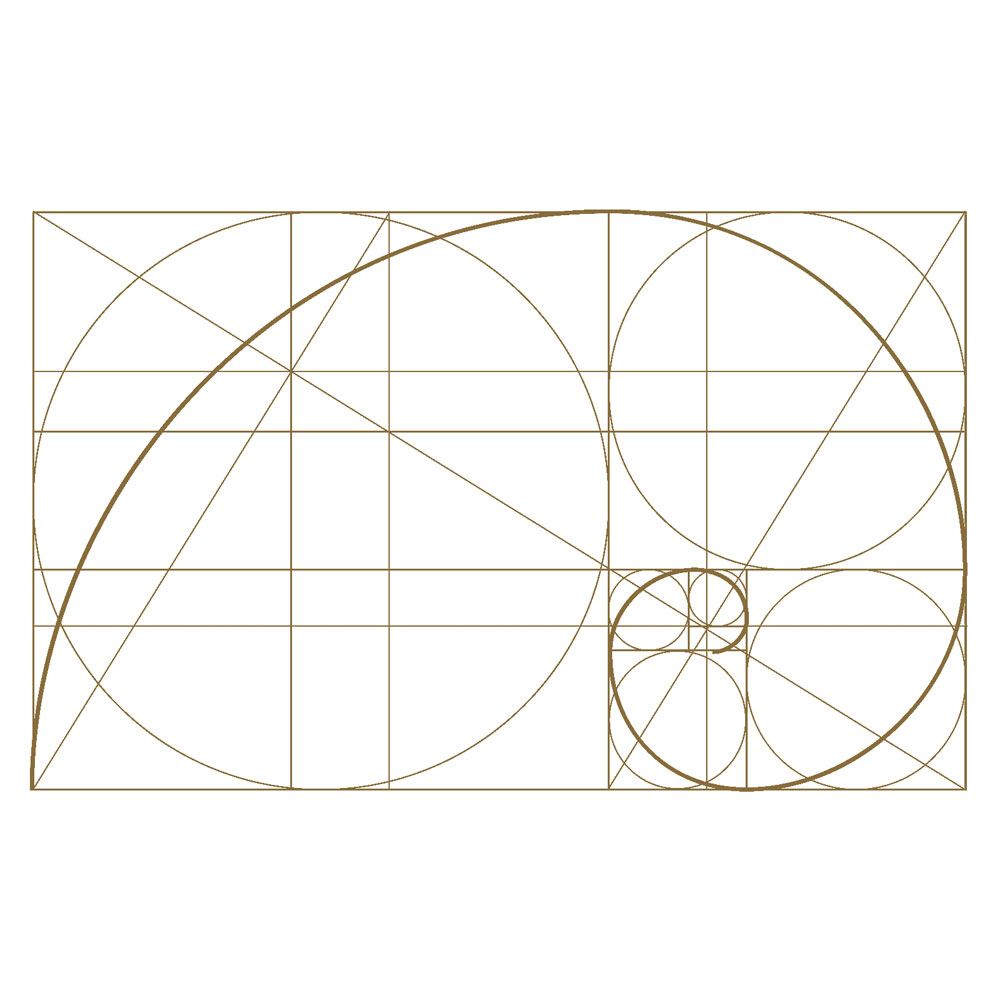
Características del número áureo
- El número áureo, también conocido como proporción áurea, es un concepto matemático que se refiere a un número irracional, aproximadamente igual a 1,618.
- Se deriva de la sucesión de Fibonacci, una serie de números donde cada número siguiente es la suma de los dos números anteriores.
- La proporción entre las dos partes es igual a 1,618. Puede utilizarse para crear un rectángulo áureo que tenga una relación de 1,618 entre la longitud y la anchura.