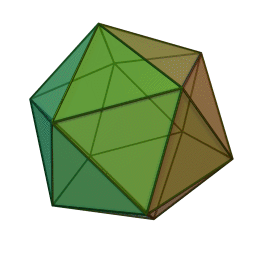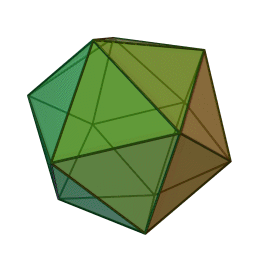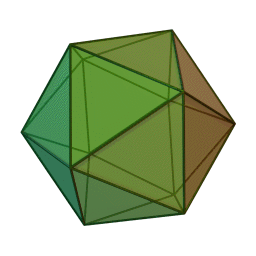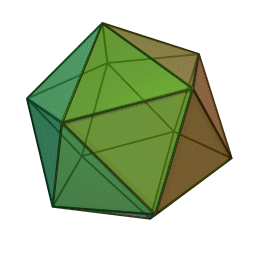
Características del icosaedro
- Un icosaedro es un sólido tridimensional que forma parte de los poliedros y tiene 20 caras.
- El término proviene del griego “icos” que significa “veinte”.
- Existen varios tipos de icosaedros, como el icosaedro regular convexo, el icosaedro rómbico, el pseudo-icosaedro, el gran icosaedro y los sólidos de Johnson.
- En el “Timeo”, Platón relacionó los cinco poliedros regulares convexos con elementos del universo.
- Consideró el icosaedro como representativo del agua debido a su gran estabilidad, gracias a su elevado número de caras y vértices en comparación con los otros cuatro poliedros.