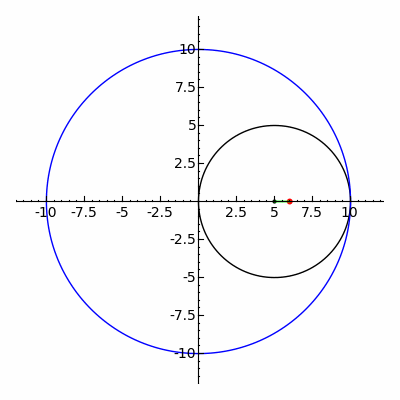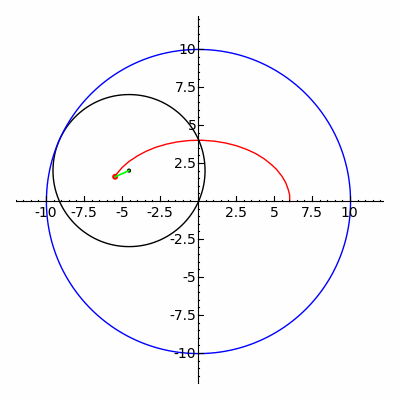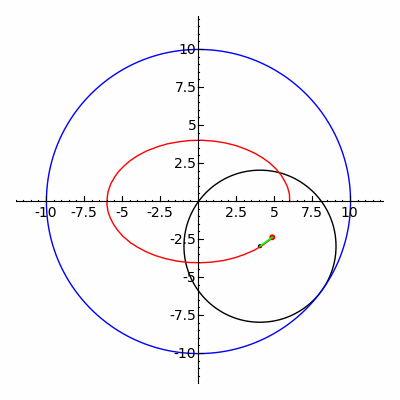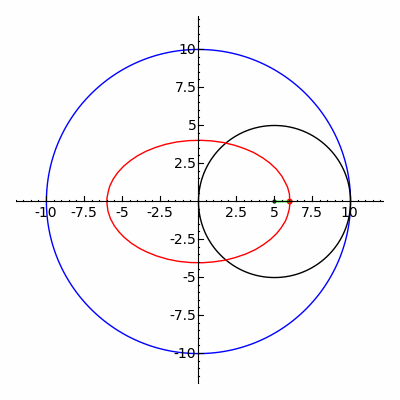
Características de la Elipse
- La elipse es una curva plana cerrada que resulta de la intersección de un cono o cilindro con un plano que corta el eje de rotación.
- Pertenece a la familia de las cónicas con una excentricidad entre 0 y 1.
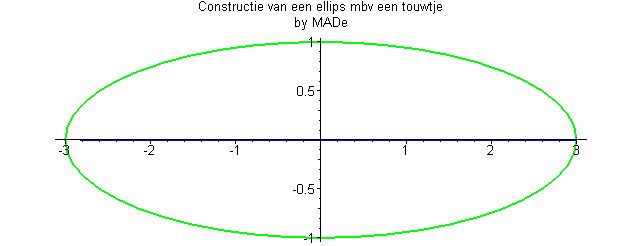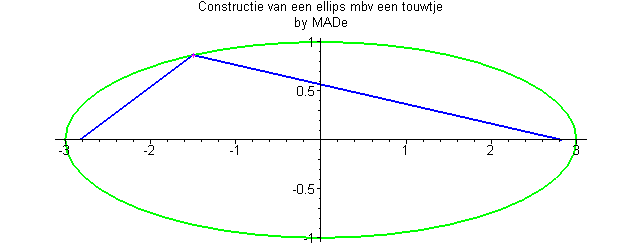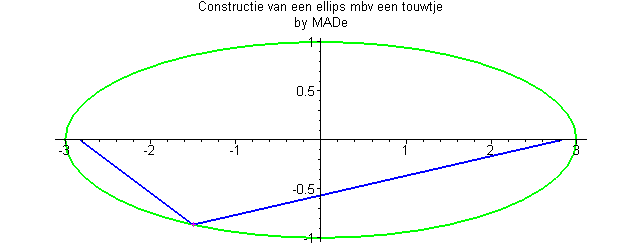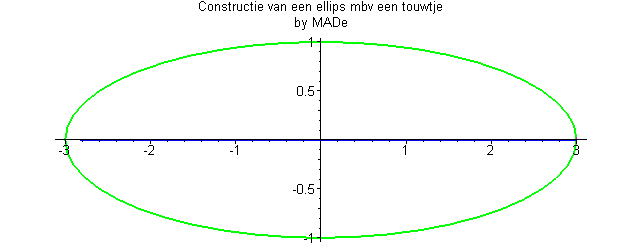
- Los puntos que forman la elipse tienen una suma de distancias a los focos constante.
- En vista de perspectiva, la elipse aparece como un círculo visto de lado o la sombra de un disco sobre una superficie plana.
- En astronomía, las elipses se utilizan para representar las órbitas de los cuerpos celestes, como la órbita elíptica de la Tierra alrededor del Sol.